Inorder traversal using a stack

First let's see how to do an inorder traversal using a stack:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14

void inorder_traverse(NODE * T)
{
        NODE * p = T;
        while (1) {
                while (p) {
                        PUSH(p);
                        p = p->L;
                }
                if (!(p = POP()))
                        break;
                visit(p);
                p = p->R;
        }
}

This function can be illustrated as:

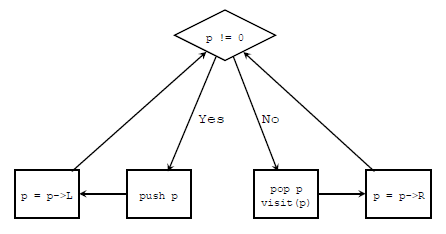
• p is the current node
• if the current is not NULL, we push it and move left
• if the current is NULL, we pop a node up, visit it and move right
• every time we move, either move left or move right, we start a new loop (just like recursion)

The key points are:

• we move left after pushing a node, so that we will pop and visit nodes from left to right
• we move right after poping and visiting a node, because the left subtree must have been manipulated

Function inorder_traverse is not hard to understand. You should have known well about it. Now let's see how Morris modified it so that no stack is needed any more.

Morris Algorithm

The following is the pseudo-C code of Morris Algorithm:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16

void inorder_Morris(NODE * T)
{
        NODE * p = T;
        while (p) {
                while (p->L) {
                        /** insert or remove thread **/
                        if (no_thread)
                                insert_thread;
                        else
                                remove_thread;
                        p = p->L;
                }
                visit(p);
                p = p->R;
        }
}

The key point is to transform the binary tree into a right-threaded binary tree temporarily and restore it later (line 7, 8, 9, 10).

A right-threaded binary tree, if you never heard of it, is a binary tree like this:

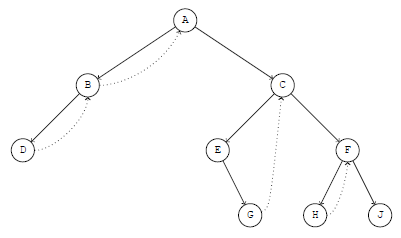
Right-threaded binary tree

As this figure shows, the NULL right child of a node P is used to point to P's inorder successor (denoted as P$). That is to say:

1. The right link of any node without a right child will be used as the start of a thread (dotted lines)
2. If a node P has a left subtree, then P is the end of a thread whose start point is $P (P's inorder predecessor). Therefore, we can add this thread (from $P to P) when reaching P and remove it after coming back to P from $P.

Let's study figure Right-threaded binary tree, which is transformed from (2). There are 4 nodes that have left subtrees: A, B, C and F, so there are 4 thread that point to them. The key point is that the nodes pointing to them are their inorder predecessors respectively: B, D, G and H. Therefore, we do not need to push A, B, C and F into stack, since we can reach them via the right links of their inorder predecessors.

This is the main idea of Morris algorithm. Now let's rewrite our inorder_traverse so that it looks more like inorder_Morris:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20

void inorder_traverse(NODE * T)
{
        NODE * p = T;
        while (p) {
                while (p->L) {
                        if (p != STACK_TOP()) {
                                PUSH(p);
                        } else {
                                p = POP();
                                break;
                        }
                        p = p->L;
                }
                visit(p);
                if (p->R)
                        p = p->R;
                else
                        p = STACK_TOP(); /* note: STACK[BASE] == 0 */
        }
}

This is a disguised inorder_traverse. It does the same thing as the first inorder_traverse, but it looks very similar with inorder_Morris so we only need to do very slight modification and an implementation of Morris algorithm will be done.

Before implementing the Morris algorithm, let's imagine all threads are inserted into the tree. It's easy to know:

• line 15 is always true (except that we have reached the last node)

• if the line from p to p->R is a thread, then p->R always points to the stack top, so we no more need a stack

• to implement Morris algorithm, we only need to replace line 7 and 9 with insert_thread code and remove_thread code respectively and we're done

• after threads are inserted into the tree, there are circles so we can always come back through the right links, so:

  • if a node has no left subtree, visit it without pushing or poping

  • if a node has a left subtree, do normal inorder traversal, except that:

    • insert right thread when push is needed
    • remove right thread when we come back (i.e. when pop is needed)

I guess you have understood Morris algorithm well, it's time to code it:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

void Joseph_M_Morris(struct node * T)
{
        /* U1. [Initialize.] */
        P = T;
        R = 0;

        while (P) { /* U2. [Done?] */
                while (1) {
                        /* U3. [Look left.] */
                        Q = P->L;
                        if (Q == 0) {
                                visit(P, preorder);
                                break; /* goto U6; */
                        }

                        /* U4. [Search for thread.] */
                        while (Q != R && Q->R != 0)
                                Q = Q->R;
                        assert(Q == R || Q->R == 0);

                        /* U5. [Insert or remove thread.] */
                        if (Q != R) {
                                Q->R = P;
                        } else {
                                Q->R = 0;
                                break;
                        }

                        /* U8. [Preorder visit.] */
                        visit(P, preorder);

                        /* U9. [Go to left.] */
                        P = P->L;
                        /* goto U3 */
                }

                /* U6. [Inorder visit.] */
                visit(P, inorder);

                /* U7. [Go to right or up.] */
                R = P;
                P = P->R;
                /* goto U2 */
        }
}

The code implements not only inorder traversal but also preorder traversal. It is not hard with the help of right threads. The key parts are U4, U5 and line 41.

I made a slides showing how this algorithm works. Please click here (it contains many figures, you may have to wait a while when it's loading).